Johannes Kepler analisou durante mais de uma década os registos de Brahe e concluiu que o Modelo Heliocêntrico era o correto, formulando três Leis:
- 1ª Lei de kepler - Lei das Elipses;
- 2ª Lei de Kepler - Lei das Áreas;
- 3ª Lei de Kepler - Lei dos Períodos.
As primeiras duas foram publicadas em 1609 no "Astronomia Nova… De Motibus Stellae Martis" (Figura 1).
A terceira lei publicada em 1619.
As Leis de Kepler explicam os movimentos observados mas não explicam a origem, o porquê, desses movimentos.
A causa dos movimentos foi explicada por Newton, através da Lei da Gravitação Universal, publicada em 1687, e de forma diferente por Einstein, com a Relatividade Geral, em 1915.
1ª Lei de Kepler - Lei das Elipses
Esta lei está relacionada com a forma das órbitas dos planetas, que ao contrário de teorias até aí aceites, não são circulares.
1ª Lei de Kepler - Lei das Elipses
O planeta em órbita em torno do Sol descreve uma elipse em que o Sol ocupa um dos focos.
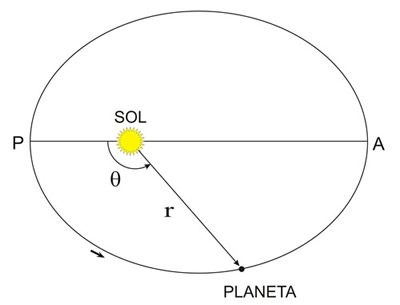
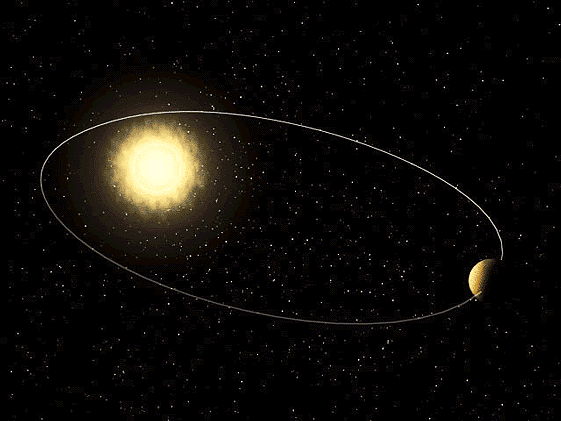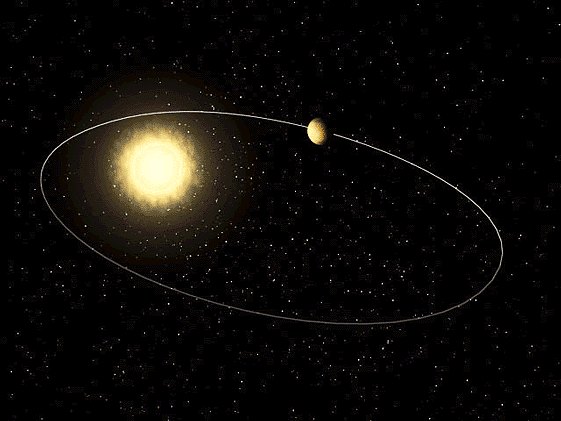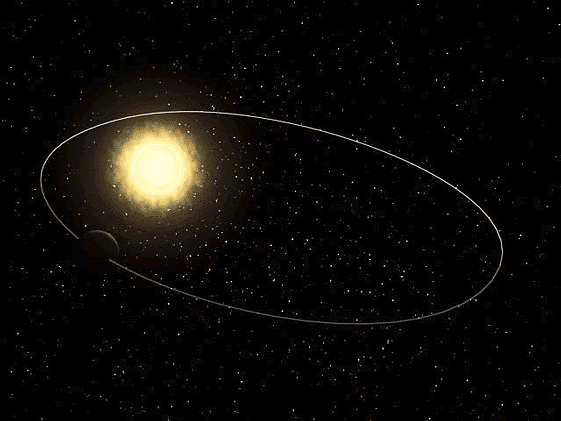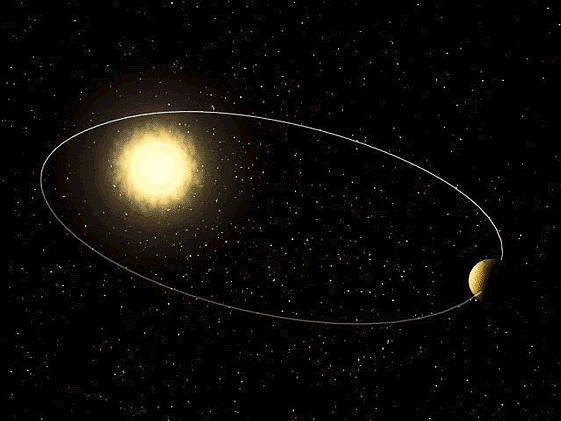
Primeira Lei de Kepler: Lei das Órbitas Elípticas
1ª Lei de Kepler
2ª Lei de Kepler - Lei das Áreas
A 2ª Lei de Kepler explica a variação da velocidade de um planeta ao longo da sua trajetória de translação.
2ª Lei de Kepler - Lei das Áreas
O vetor posição do planeta relativamente ao Sol varre áreas iguais da elipse em tempos iguais.
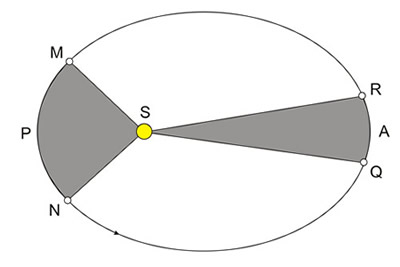
A consequência desta Lei é que velocidade com que um planeta se move ao longo da trajetória varia ao longo da sua órbita. No periélio (ponto da órbita mais perto do Sol, ponto P da Figura 4) o planeta move-se mais rapidamente e no afélio (ponto da órbita mais afastado do Sol, ponto A da Figura 4) move-se mais devagar.
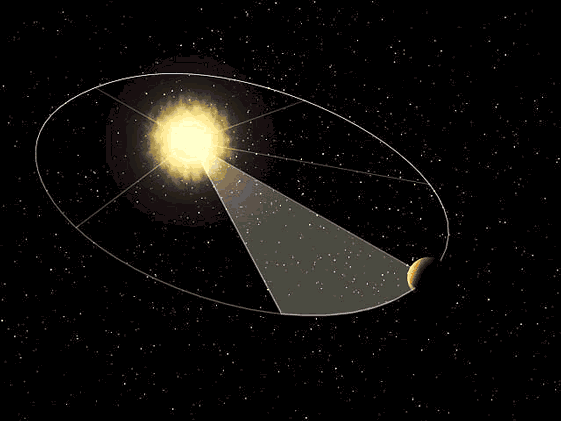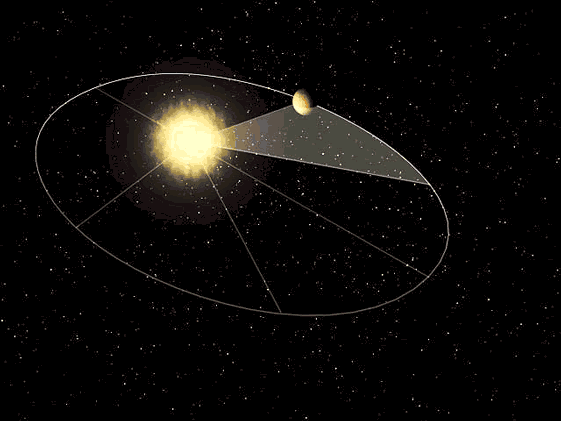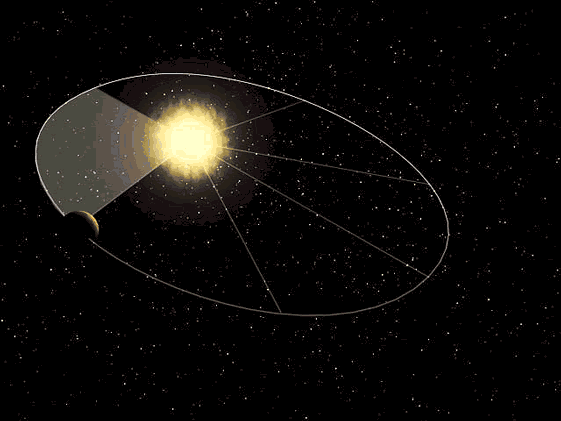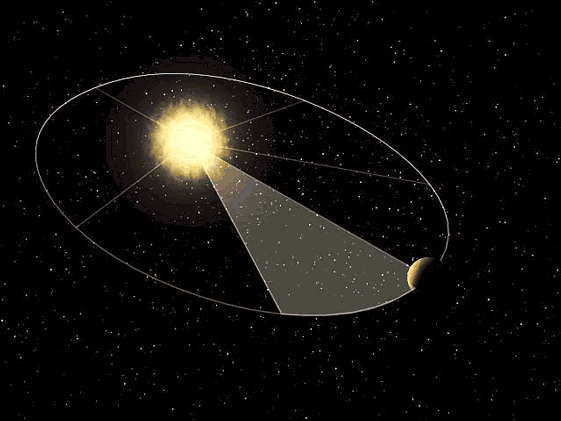
Segunda Lei de Kepler2ª Lei de Kepler
3ª Lei de Kepler - Lei dos Períodos
A última Lei de Kepler relaciona a distância a que um planeta está do Sol com o tempo (período) que demora a percorrer a sua órbita.
3º Lei de Kepler - Lei dos Períodos
O quadrado do período de revolução, \(T\), de um planeta é proporcional ao cubo do semi eixo maior, \(r\), da sua órbita.
$$\frac{T^{2}}{r^{3}}=k$$
em que:
\(T\) – período de revolução (s)
\(r\) – semi eixo maior da órbita (m)
\(k\) – constante de Kepler (s2 m-3)
Ou seja, quando mais longe do Sol estiver a órbita de um planeta, mais tempo demora a realizar a sua translação.
|
Exemplo: Calcular o período de translação de Saturno sabendo que este planeta está, em média, 9,558 vezes mais afastado do Sol que a Terra. Pela 3ª Lei de Kepler: $$\frac{{T}^{2}_{Terra}}{{r}^{3}_{Terra}}=k=\frac{{T}^{2}_{Júpiter}}{{r}^{3}_{Júpiter}}$$ (a constante \(k\) é igual porque a Terra e Júpiter estão em translação em torno do mesmo corpo (Sol)) então $${T}_{Júpiter}=\sqrt{\frac{{T}^{2}_{Terra} \times {r}^{3}_{Júpiter}}{{r}^{3}_{Terra}}}$$ Como \(T_{Terra}\) = 1 ano e, pelos dados fornecidos, como \(r_{Terra}\) = 1 ua, então \(r_{Júpiter}\) = 9,558 ua Substituindo os valores na expressão deduzida, $${T}_{Júpiter}=\sqrt{\frac{{1}^{2} \times {9,558}^{3}}{{1}^{3}}}$$ \(T_{Júpiter}\) = 29,5 anos |
A constante de Kepler é igual para todos os corpos que orbitam um mesmo astro. No caso do Sistema Solar, o valor desta constante, \({k}_{Sistema Solar}\), é igual para todos os astros que orbitam o Sol e é igual a 2,99 × 10-19 s2 m-3.
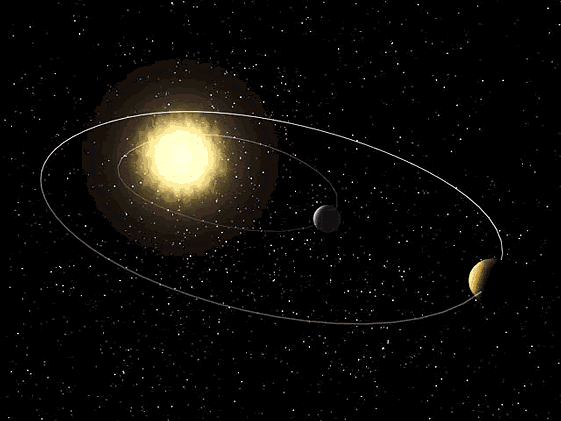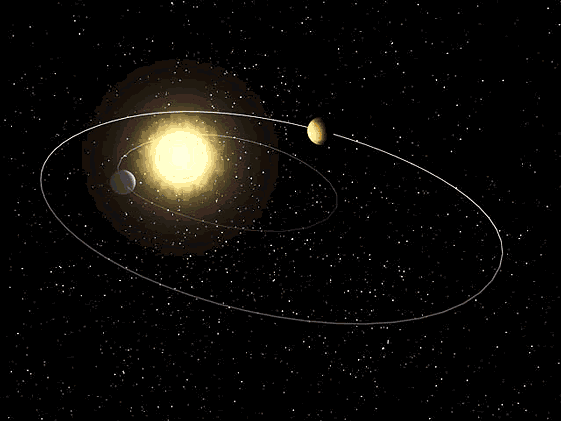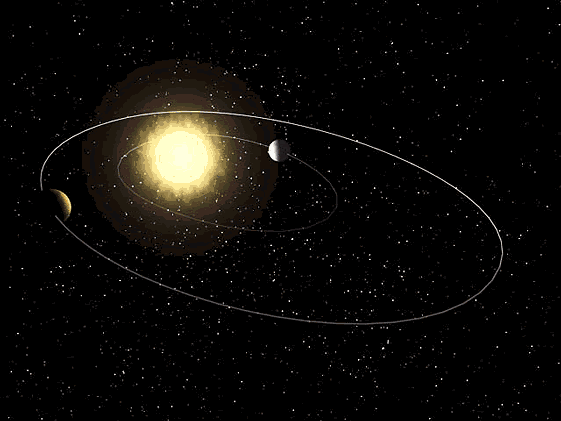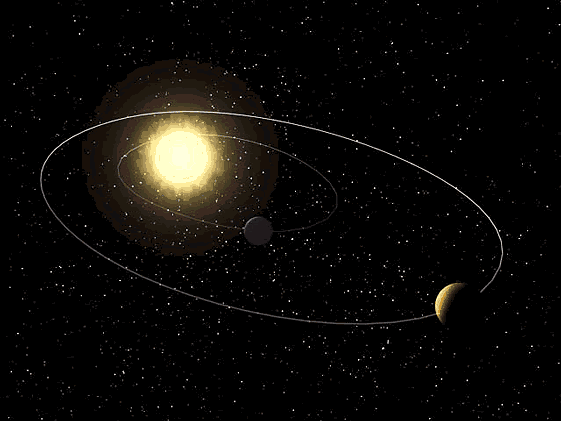
3ª Lei de Kepler – planetas interiores3ª Lei de Kepler – planetas exteriores
Bibliografia
G. Ventura, M. Fiolhais, C. Fiolhais, J. A. Paixão, R. Nogueira e C. Portela, “Novo 12F”, Texto Editores, Lisboa, 2017.
M. Alonso, E. J. Finn, “Física”, Escolar Editora, 2012, Lisboa.