Esta lista apenas contém expressões matemáticas normalmente úteis em Física e em Química.
Legenda:
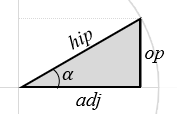
\(A\) – área; \(P\) – perímetro; \(V\) – volume; \(a\), \(b\) e \(c\) – comprimento do lado ou aresta; \(h\) – altura; \(r\) – raio; \(op\) – lado oposto ao ângulo \(\alpha\); \(adj\) – lado adjacente ao ângulo \(\alpha\); \(hip\) – hipotenusa do triângulo.
Área, perímetro e volume
|
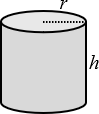
Cilindro |
|
|
|
\(A= 2 \; \pi \; r \; h + 2 \; \pi \; {r}^{2}\) \(V=\pi \; {r}^{2} \; h\) |
|
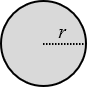
Circunferência |
|
|
|
\(A=\pi \; {r}^{2}\) \(P=2 \; \pi \; r\) |
|
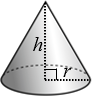
Cone |
|
|
|
\(V=\frac{1}{3} \; \pi \; {r}^{2} \; h\) |
|
Cubo |
|
|
|
\(A=6{a}^{2}\) \(V={a}^{3}\) |
|
Esfera |
|
|
|
\(A= 4 \; \pi \; {r}^{2}\) \(V=\frac{4}{3} \; \pi \; {r}^{3}\) |
|
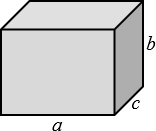
Paralelepípedo |
|
|
|
\(A=2(ab+ac+bc)\) \(V=a \; b \; c\) |
|
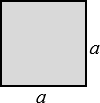
Quadrado |
|
|
|
\(A={a}^{2}\) \(P=4a\) |
|
Retângulo |
|
|
|
\(A=a \; b\) \(P=2a + 2b\) |
|
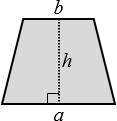
Trapézio |
|
|
|
\(A=\frac{a+b}{2} \; h\) |
|
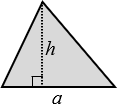
Triângulo |
|
|
|
\(A=\frac{a \; h}{2}\) |
Trigonometria
| Seno, cosseno e tangente | |
|
|
\(sin \; \alpha=\frac{op}{hip}\) \(cos \; \alpha=\frac{adj}{hip}\) \(tg \; \alpha=\frac{sin \; \alpha}{cos \; \alpha}=\frac{op}{adj}\) \(sin \; {x}^{2}+cos \; {x}^{2}=1\) |
Produto escalar
|
\(\vec{a}\cdot\vec{b}\;=\;\mid a \mid\;\mid b \mid \cos \theta\) em que: \(\vec{a}\cdot\vec{b}={a}_{x}\;{b}_{x}+{a}_{y}\;{b}_{y}+{a}_{z}\;{b}_{z}\) |
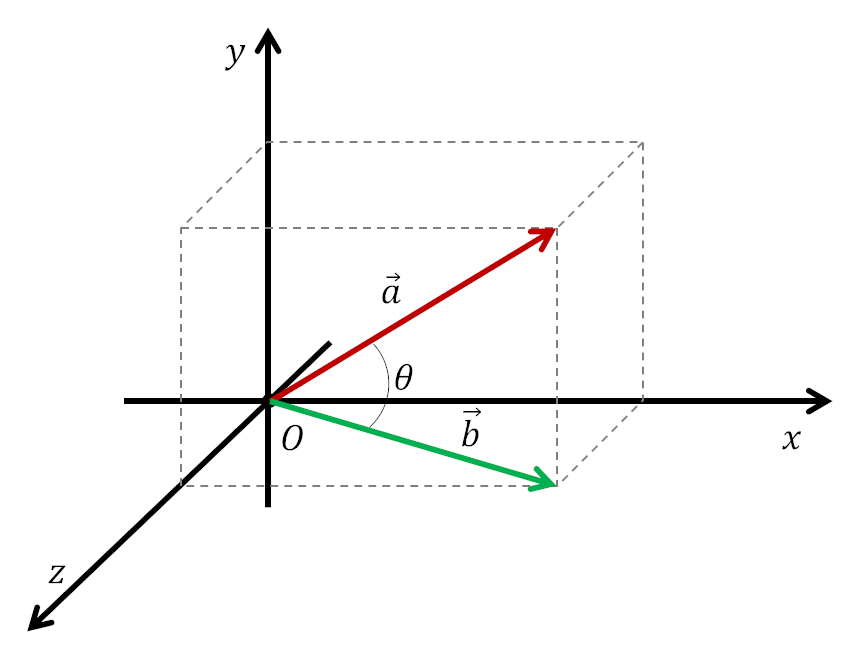
|
Produto vetorial
|
O produto vetorial entre os vetores \(\vec{a}\) e \(\vec{b}\) representa-se por $$\vec{a} \times \vec{b}$$ ou $$\vec{a} \wedge \vec{b}$$ e é um outro vetor, \(\vec{c}\), com direção perpendicular ao plano definido por \(\vec{a}\) e \(\vec{b}\), e com sentido que é dado pela regra da mão direita (ver figura 2) e cujo módulo é igual a $$\vec{a} \times \vec{b}\;=\;\mid a \mid\;\mid b \mid \sin \theta$$ em que: O produto vetorial é importante para o cálculo da força magnética. |

|